Jak matematyka pozwala zrozumieć procesy 3D?

  • Post category:blog

Jak matematyka pozwala zrozumieć procesy 3D?

Królowa nauk – matematyka – przydaje się w wielu różnych dziedzinach naszego życia, choć często nie zdajemy sobie z tego faktu sprawy. Umiejętność liczenia i rozwiązywania zawiłych zadań jest przydatna nie tylko w ekonomii, bankowości czy księgowości. Jak zastosowanie matematyki pozwoli na lepsze zrozumienie procesów 3D i inżynierii odwrotnej?

Odwzorowanie odwrotne funkcji a inżynieria odwrotna

Inżynieria odwrotna, inaczej reverse engineering nazywana jest również inżynierią wsteczną. To dziedzina wiedzy leżąca u podstaw procesów 3D. W ramach inżynierii odwrotnej można stworzyć trójwymiarową dokumentację fizycznie istniejącego obiektu czy jego elementu. W dzisiejszych czasach coraz rzadziej dokonuje się fizycznych pomiarów np. obiektów budowlanych, a następnie nanosi się je w programie do projektowania 3D. Wykorzystuje się za to skanning 3D, który pozwala na uzyskanie dużej ilości danych potrzebnych do wiernego odzwierciedlenia detali przy użyciu sugerowanego do inżynierii odwrotnej oprogramowania.

W wyniku pracy można uzyskać model w formacie STL, IGS lub STP. STL to skan w formie siatki trójkątów, która wymaga dalszej obróbki w oprogramowaniu 3D. IGS to powierzchniowy model automatycznie generowany, możliwy do zaimportowania w programach typu CAD. Natomiast w formacie STP mamy do czynienia z parametrycznym modelem, który można edytować w oprogramowaniu CAD.

Dla wygenerowania obrazu wirtualnego z elementu istniejącego w rzeczywistości stosuje się w inżynierii odwrotnej zasady funkcji odwrotnych i ich odwzorowania, znane z matematyki. Funkcja przyporządkowująca wartościom, w tym przypadku punktom gromadzonym przy skanowaniu 3D, jakiejś funkcji jej odpowiednich argumentów, czyli działanie odwrotne do samej funkcji. Najłatwiej można to zrozumieć w ten sposób, że jeśli każdemu elementowi x ze zbioru X przyporządkowane są różne elementy y ze zbioru Y za pomocą funkcji, to można równie dobrze każdemu elementowi y ze zbioru Y przyporządkować dokładnie jeden element x ze zbioru X tak, że obrazem x w odwzorowaniu odwrotnym funkcji jest y.

Przetwarzanie obrazu przez skaner 3D

Skaner 3D pozwala na odwzorowanie odwrotne dowolnego obiektu, nawet budynku czy postaci ludzkich. Jego praca opiera się na zastosowaniu matematyki w działaniu i przetwarzaniu gromadzonych informacji.

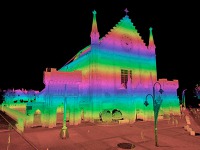
Podczas skanowania 3D dokonywana jest analiza rzeczywistego obiektu dążąca do wygenerowania danych, które pozwolą na jego opis i przetransferowanie go do programu komputerowego. Zgromadzone dane są przetwarzane i wykorzystywane do konstruowania modeli 3D, które umożliwiają jak najwierniejsze odwzorowanie otoczenia. To zwykle laserowe skanery 3D, które emitują promień lasera, który odbija się od punktów w skanowanej przestrzeni, a następnie natychmiast wraca do urządzenia. Dokonywany jest pomiar odległości punktu od sprzętu. W ten sposób powstaje chmura punktów – model 3D w orientacji 360 stopni.

Czytaj także: Druk 3D, a świadomość jego wykorzystania

Wektory i bryły – matematyka w drukarce 3D

Przy przygotowywaniu modelu do wydruku z wykorzystaniem drukarki 3D tworzone są modele w formacie STL, czyli brył i wektorów. Powierzchnie obiektów są zbudowane z trójkątów. Najprostszą z brył, jaką można opisać w ten sposób jest czworobok składający się z czterech trójkątów, z których każdy jest jedną ścianą. Każdy z trójkątów w formacie STL ma trzy krawędzie łączące się ze sobą w węzłach, natomiast narożniki można łączyć jedynie w węzłach.

Geometria 3D to najbardziej widoczne dla projektanta połączenie zagadnień matematycznych z inżynierią odwrotną. Programowanie drukarek 3D opiera się na takim łączeniu trójkątów, by powstały projekt można było wydrukować z dokładnością do najmniejszego szczegółu.

Przetwarzanie chmury punktów

Chmura punktów jest określeniem stosowanym w procesach 3D i w inżynierii odwrotnej. Oznacza ona wielomilionowy zbiór takich punktów, który jest geometryczną reprezentacją skacowanego obiektu. Uzyskuje się ją poprzez fotogrametrię lub skanowanie laserowe 2D.

Zobacz kilka modeli skanerów dostępnych w naszym sklepie:

Do przetworzenia chmury punktów zgromadzonych dzięki procesowi skanowania trójwymiarowego dochodzi w ramach modelowania 3D. Proces ten polega w istocie na stworzeniu matematycznej interpretacji powierzchni dowolnego obiektu, zaś płaszczyzna jest przedstawiana w trójwymiarze. Operator programu do modelowania 3D powinien przetwarzać chmurę punktów, w której zgromadzone są informacje dotyczące lokalizacji wielomilionowych punktów w przestrzeni trójwymiarowej, zapisane za pomocą układu współrzędnych X, Y i Z. Tak zapisane informacje są przekazywane do specjalistycznych systemów, które konstruują model przestrzenny skanowanych elementów.

Czytaj także: Fotografia, a drukowanie 3D